Ein einfaches Experiment beweist: π = 4

Die übliche Reaktion auf meine Darstellung oben lautet, dass beim Grenzwert nach seiner derzeitigen Definition die Gesamtlänge der Stufen den Kreisbogen nie erreicht. Denn selbst bei einer unendlich großen Zahl an Schritten bleibt immer noch ein realer Abstand zwischen der Kreislinie und den einzelnen Stufen. Diesen Abstand können wir auch beim Grenzwert noch aufsummieren, dadurch ist die Summe der Stufen-Strecken stets höher als die Länge der Kurve. Aber nicht die Summe der Stufen-Strecken wird der Kurve angenähert; die Kurve wird den Kreissehnen angenähert. In anderen Worten: Es sind die Hypotenusen der kleinen Dreiecke, die gegen die Kurve konvergieren, nicht die Summe der anderen Seiten des Dreiecks.

Obwohl mir bewusst ist, dass es sich hier um die gängige Meinung handelt, kann ich ihr nicht zustimmen. In meiner Arbeit über die newtonschen Hilfssätze (zu finden auf meiner Webseitehttp://tinyurl.com/h9kxaal) habe ich nachgewiesen, dass die Tangente seines Dreiecks am Grenzwert länger sein muss als die Kreissehne und damit der Kreisbogen. Wenn wir das auf dieses Problem umlegen, bedeutet das, der Kreisbogen kann sich der Kreissehne des Grenzwerts gar nicht annähern. Die Tangente ist laut Newtons eigener Definition in der Principia ein Teil des Kreisbogens. Wenn also die Tangente am Grenzwert länger ist als die Kreissehne, muss das auch für den Kreisbogen gelten.

Das heißt, die Kurve nähert sich in keinem Fall den Hypotenusen der Stufen an, egal wie viele es sind. Die Hypotenusen sind die Kreissehnen und sowohl Kreisbogen als auch Tangente konvergieren nicht gegen sie.

Sie wollen nun sicher wissen, wo in der Principia Newton schreibt, der Kreisbogen bestünde aus Tangenten. An derselben Stelle, an der er erklärt, die Kreisbewegung bestünde aus den Vektoren der zentripetalen Beschleunigung und der Eigenbewegung eines Körpers. Newton definiert nur diese beiden Bewegungen, und er ordnet die Eigenbewegung des Körpers explizit der Tangente zu.

Damit können aber die historischen und gegenwärtigen Interpretationen nicht korrekt sein. Die Hypotenusen konvergieren nicht gegen Kurve oder Kreisbogen. Wie in der Abbildung gezeigt, nähert sich die Tangente dem Kreisbogen an, allerdings nur, wenn die Tangentenlänge gleich dem Radius ist. Das wiederum ist nur der Fall, wenn das Segment einem Achtel des Kreises entspricht. Die Annäherung erfolgt dann genau wie in meinen Arbeiten beschrieben, weil der Kreisbogen auch am Grenzwert niemals eine stetige Kurve ist.

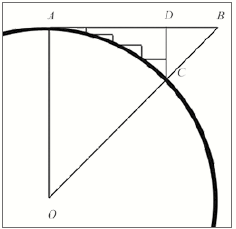
Ein Kreisbogen ist definiert als eine aus geraden oder linearen Vektoren bestehende Kurve und kann daher nicht stetig sein, sofern wir unter „stetig“ verstehen, dass zurückgelegter Weg oder vergangene Zeit gegen null gehen. Logischerweise können Weg und Zeit nicht gegen null gehen, da es bei null weder Weg noch Zeit gibt. Alle Zahlen in der Mathematik und Physik beinhalten ein Differenzial; und weil das so ist, kann eine Kurve auch nicht als ununterbrochen in diesem Sinne gelten. Eine Kurve muss auch am Grenzwert als Ergebnis linearer Vektoren betrachtet werden.

Da dies so sein muss, muss auch stimmen, dass sich der von mir in der Abbildung gezeichnete Weg dem Kreisbogen annähert, und zwar aus genau den von mir genannten Gründen. Der Weg nähert sich dem Kreisbogen in dem Sinne an, als er tatsächlich näher an den Bogen herankommt. Das zumindest kann niemand abstreiten. Weil aber der Kreisbogen nicht einmal am Grenzwert stetig ist, konvergiert der Weg tatsächlich gegen den Kreisbogen, je mehr Stufen wir einzeichnen.

Weil sich aber die Streckenlänge nie ändert, egal wie viele Stufen wir zeichnen, muss die Tangente gegen den Kreisbogen konvergieren. Oder, betrachtet man einen Achtel eines Kreises, muss die Tangente schlicht der Kreisbogen sein.

Quelle: redaktionelle Aufbereitung der Webseite http://milesmathis.com/pi3.html

Anmerkung zu „Die Vernichtung von Pi“

Viele Leser, besonders jene, die gerade erst auf meine Arbeiten gestoßen sind, werden bei diesem Artikel früher oder später in eine gedankliche Sackgasse geraten. Wer tatsächlich mit diesem Artikel beginnt, kommt höchstwahrscheinlich zu dem Schluss, ich würde die Integrale falsch berechnen. Diesen Menschen möchte ich entgegnen, dass nicht ich es bin, der die Integrale falsch berechnet. Newton und Leibniz und Cauchy und alle Mathematiker danach haben die Integrale falsch berechnet. Indem ich drei bedeutende Arbeiten über die Grundlagen der Infinitesimalrechnung schrieb, habe ich mir das Recht erarbeitet, diesen Artikel hier zu schreiben.

Der erste Artikel¹ zeigt auf, dass die Ableitungsfunktion von Beginn an falsch definiert wurde. Die Ableitung ist ein konstantes Differenzial in einem Teilintervall und kein bei der Annäherung an null unendlich klein werdendes Differenzial. Die Annäherung an null in der Differenzialrechnung ist unnötig und das Intervall der Ableitung ist eine real existierende Differenz. In jedem spezifischen Problem findet sich auch Zeit, die im Intervall der Ableitung vergeht. In der Differenzialrechnung ist also ebenfalls nichts momentan. Das revolutioniert die Quantenelektrodynamik, weil dadurch das Idealteilchen ausgeschlossen und die Notwendigkeit der Renormierung umgangen wird.

Der zweite Artikel² beweist, dass die ersten acht Hilfssätze oder Annahmen von Newton in der Principia Mathematica alle falsch sind. Newton betrachtet bei der Annäherung an den Grenzwert den falschen Winkel seines Dreiecks. Dadurch zieht er falsche Schlüsse bezüglich der Winkel sowie über die Tangenten- und Bogenlänge des Grenzwerts.

Der dritte Artikel³ schließlich setzt sich gründlich mit den historischen Beweisführungen für die Kreisbeschleunigungsformel a = v2/r auseinander. Die Arbeit umfasst auch die Beweisführung von Newton und Feynman und zeigt, dass sie alle fundamentale Fehler enthielten. Die derzeit gültige Gleichung dafür wird ebenso wie die Formel für die Kreisgeschwindigkeit v = 2πr/t falsifiziert.

Wem also der Artikel hier zu ungenau oder zu wenig mathematisch ist, sollte diese Arbeiten lesen, bevor das alles als „eine Nummer zu groß“ abgetan wird. Ich kann unmöglich in jeder Arbeit alle meine Beweise herleiten oder alle meine Argumente aufzählen. Ich fürchte also, wer sich wirklich überzeugen lassen will, wird noch etwas weiterlesen müssen.

Dieser Artikel baut allerdings auf die in den anderen Arbeiten enthaltenen Änderungen historischer Formeln auf, das muss ich an dieser Stelle zugeben.

Endnoten

1. Mathis, Miles: „A Redefinition of the Derivative: Why the Calculus Works – and Why it Doesn't“, 2002, 2003, 2004; http://tinyurl.com/j4ums88
2. Mathis, Miles: „A Disproof of Newton's Fundamental Lemmae“, 2005; http://tinyurl.com/h9kxaal
3. Mathis, Miles: „A Correction To The Equation a = v2/r (and a Refutation of Newton's Lemmae VI, VII & VIII)“, 2004; http://tinyurl.com/hsp6naa

Quelle: redaktionelle Aufbereitung der Webseite http://milesmathis.com/pi2.html