Ein einfaches Experiment beweist: π = 4

Sie fragen sich sicher, wofür wir die Integralrechnung brauchen? Weil wir, um dieses Problem zu lösen, die Geradenaundbmit der Zeittintegrieren müssen. Anders gesagt: Wir integrieren nichtaundb. Wir integrierenamittund dannbmit demselben Wert vont. Falls Ihnen das Wort „integrieren“ nicht zusagt – weil es sich dabei um einen Begriff der Infinitesimalrechnung handelt – lassen Sie es mich so ausdrücken: Wir müssen nachvollziehen, wie sich erstaund dannbim Zeitraumtändern. So berücksichtigen wir auch den Zeitfaktor dieses Problems.

Versuchen Mathematiker oder Physiker gegenwärtig, das Problem mittels Integralrechnung zu lösen, lassen sie die Zeit mehr oder weniger außen vor und messenaim Verhältnis zub. Sie integrieren Bewegungamit Bewegungb, um Bewegungczu erhalten. Bewegungcentspricht derc-Geraden. Doch obwohl die genutzte Berechnungsmethode an sich korrekt ist, wird sie falsch umgesetzt. Da die gesamte Physik im Prinzip angewandte Mathematik ist, muss die Mathematik jedoch richtig angewandt werden. Wird die richtige Berechnungsmethode falsch eingesetzt, liefert sie trotz allem ein falsches Ergebnis.

In meinen anderen Arbeiten habe ich daher Rollkurven-Berechnungen als Lösung vorgeschlagen. Eine Rollkurve ist ein zyklischer oder rollender Kreis. Rollkurven-Berechnungen sind an dieser Stelle hilfreich, weil sie explizit die Zeit miteinbeziehen. Die Berechnungsmethode integriert die drei Variablen a, b und t. Darüber hinaus werden die Variablen in der Rollkurven-Berechnung auch richtig eingesetzt. Wir müssen also nur noch die Rollkurven-Berechnung nehmen und sie auf der Strecke entlang der Kreisbahn anwenden. Das löst unser Problem perfekt und liefert uns die richtige Antwort: Der Umfang eines Kreises ist 8r.

Warum funktioniert die Rollkurven-Berechnung hier? Die Bewegung entlang einer Kreislinie gleicht der Bewegung entlang der Außenseite eines um seinen Mittelpunkt rotierenden Kreises. Anders ausgedrückt: Stellen Sie sich ein großes, sich drehendes Hamsterrad vor, das fixiert ist und sich daher nicht vorwärtsbewegt. Es dreht sich einfach auf der Stelle. Sie befinden sich an einer beliebigen Stelle an der Außenseite des Rads. Während sich das Rad dreht, drehen Sie sich ebenfalls – nun vollführen Sie eine Kreisbewegung. Genau das bildet die moderne Rollkurven-Berechnung ab.

Warum Pi falsch ist

Unabhängig davon versteht ein Großteil der Menschen nicht, wie ich auf die Idee kam, so etwas infrage zu stellen. Ich bin kein berühmter Quantenphysiker oder Wissenschaftler der NASA. Und ich gebe zu, ich hatte keine Ahnung von den Problemen in der Quantenphysik und Raketenforschung, als ich dies berechnete. Sie waren nur eine nachträgliche Bestätigung der Fakten. Ich wusste nichts über von Brauns Probleme mit den Gleichungen, bis ich meine Arbeiten über Pi geschrieben hatte. Die Verbindung zur Rollkurven-Berechnung – wo Pi ebenfalls gleich 4 ist – entdeckte ich erst einige Jahre später. Wie also konnte ich ein Problem lösen, von dem ich gar nicht wusste, dass es existierte?

Nun, ich kam über Umwege dorthin, als ich damit zusammenhängende Probleme lösen sollte. Und ein Zusammenhang zwischen den Problemen war vorhanden. Doch niemand wusste davon, bis ich ihn aufzeigte. Ich arbeitete damals an Newtons Gleichungen zur Umlaufbahnbestimmung, die meiner Meinung nach einige Unklarheiten aufwiesen. Anders ausgedrückt: Sie ergaben für mich keinen Sinn. Newtons Beweise waren in meinen Augen ziemlich lückenhaft und die neueren Versionen der Beweisführung durch Größen wie Dr. Richard Feynman erschienen mir um nichts besser. Tatsächlich konnte ich sogar nachweisen, dass diese schlechter waren.

Da es sich bei einer Umlaufbahn nur um eine Bewegung entlang eines Kreises handelt, lässt sich der Zusammenhang einfach erkennen. Ich begann also noch einmal ganz von vorne und löste Newtons Gleichungen ein zweites Mal, diesmal mit ein paar Korrekturen. Die Korrekturen lösten viele Probleme, aber nicht alle. Doch ich sollte erst ein paar Jahre später auf den Gedanken kommen, Pi selbst genauer zu betrachten.

Meine Korrekturen an den Gleichungen zur Bahnbestimmung deuteten darauf hin, dass der Wert von Pi einfach nicht korrekt war. Wie sich herausstellte, basierten die alten Gleichungen zur Bahnbestimmung – auch jene von Newton – auf der euklidischen Geometrie, die Zeit außen vor ließ. Die in der Schule gelehrte Geometrie berücksichtigt keine Geschwindigkeiten. Sie umfasst nur Distanzen. Wird Pi mithilfe der Geometrie – ohne Zeit und Geschwindigkeiten – berechnet, lautet das Ergebnis tatsächlich 3,14 … In der Physik ist diese Art der Berechnung jedoch unbrauchbar. In der Physik gibt es fast immer eine Bewegung, die nachvollzogen werden soll. Zeit spielt also immer eine Rolle. Jede Streckenlänge muss durch eine Geschwindigkeit ersetzt werden. Und sobald Sie das tun, können Sie die euklidische Geometrie nicht mehr nutzen. Sie enthält einfach nicht genug Variablen – man hat immer eine Variable zu wenig.

Das bedeutet aber auch, die alten Berechnungen zur Umlaufbahnbestimmung hatten immer eine Variable zu wenig. Sie waren unvollständig, in ihnen fehlte die Zeit. Weil in den Berechnungen aber die Zeit fehlte, konnten sie die Realität nicht abbilden. Sie funktionierten nur für ein theoretisches Konstrukt, wo alles in einem einzigen imaginären Moment stattfand. Am Ende wurden dadurch alle Berechnungen unlösbar.

In der Quantenmechanik gibt es die sogenannte Renormierung. Dieses Verfahren wird dort für nicht lösbare Gleichungen angewendet. Vereinfacht gesagt: Sollen Probleme aus der Realität mit Gleichungen ohne ausreichende Berücksichtigung der Zeitvariablen berechnet werden, liefern die Gleichungen nur null oder unendlich als Lösungen. In der Quantenmechanik ist das bei allen Gleichungen der Fall. Das gestehen die Forscher ein, wissen aber nicht, warum. Anders formuliert versuchen sie, kinematische Probleme mit Geometrie zu lösen. Das ähnelt dem Versuch, ein Ölgemälde mit dem Bleistift zu malen.

Entsprechend können auch keine physikalischen Probleme mit Geometrie gelöst werden, da auch dafür die Zeitvariable fehlt. Zwar wird versucht, die Zeit am Ende irgendwie wieder in die Berechnungen einzufügen, doch dies hat noch nie funktioniert.

Quelle: überarbeitete Version des vollständigen Artikels auf der Webseite http://milesmathis.com/pi7.pdf

Die Vernichtung von Pi: Kurzfassung

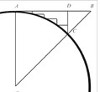
Gegeben ist ein Kreissegment entsprechend der Abbildung mit AO = AB. Damit ist der Winkel bei B gleich 45 Grad und es gilt DB = DC.

Daraus folgt durch Substitution AD + DC = AB. Die Strecke AD + DC kann auch als jede beliebige Zahl an Teilstrecken dargestellt werden, wie in der Abbildung eingezeichnet. Hier ist der Weg in vier Teilstrecken gegliedert, die uns in vier Stufen von A nach C bringen.

Der neue Weg, vorgegeben von den Teilstrecken, hat dieselbe Länge wie AD + DC. Das ist auch bei flüchtiger Betrachtung erkennbar. Sie liegt näher am Kreisbogen AC, doch die Länge entspricht immer noch der Originalstrecke AD + DC.

Unterteilen wir den Weg in acht Teilstücke statt in vier, bleiben wir noch näher am Kreisbogen, behalten aber wieder die ursprüngliche Länge von AD + DC bei.

Wenn wir uns mit diesem Verfahren Richtung Grenzwert bewegen, nähern wir unseren Weg dem Kreisbogen AC an. Das muss also bedeuten, die Länge des Kreisbogens AC ist gleich der Streckenlänge AD + DC. Aufgrund der Substitutionsregeln bedeutet das: AC = AB.

Da ein Kreis aus acht solchen Bögen besteht, ergibt sich daraus der Umfang des Kreises mit 8AB.

Weil AB = AO und AO dem Radius entspricht, lautet die Formel also U = 8r.

Pi kommt in der Kreisgleichung hier nicht vor und wurde somit ausgelöscht.

Einige mögen nun einwerfen, meine Berechnungen seien falsch. Ich behaupte jedoch, nicht ich, sondern alle bisherigen Mathematiker haben falsch gerechnet.