Sowohl in der Raketenforschung als auch in der Quantenmechanik traten in Zusammenhang mit Pi große Probleme auf. Vor mir hatte jedoch noch niemand Pi selbst infrage gestellt.
In der Raumfahrt stellten die Techniker von Beginn an ein Versagen ihrer theoretischen Gleichungen in der Praxis fest. Ende der 1950er Jahre gestanden Wissenschaftler des amerikanischen Raumfahrtprogramms unter der Leitung von Dr. Wernher von Braun massive Fehler in ihren Berechnungen ein. Die Raketen waren einfach nicht dort, wo sie sein sollten – allerdings nur,wenn gekrümmte Flugbahnen im Spiel waren. Die ersten Raketen in der Erdumlaufbahn wiesen massive Verspätungen auf, was auf Berechnungsfehler von über 20 Prozent hindeutete. Die Russen standen vor demselben Problem.
In den Pressemitteilungen verwiesen sie – und tun das immer noch – auf ein mögliches Treibstoffproblem. Hinter den Kulissen aber untersuchten sie andere Möglichkeiten. Heute wird das Versagen der Gleichungen Dunkler Materie zugeschrieben. In den 1960er Jahren fragten sich die Wissenschaftler, ob das Problem mit den Raketen von unbekannten Äthern oder anderen Naturgewalten stammen könnte. Wie sich herausstellte, entsprechen die Fehler in den Gleichungen genau der Differenz zwischen Pi und 4.
Ein ganz ähnliches Problem zeigte sich in der Quantenmechanik. Da sich Quanten oft auf Umlaufbahnen oder gekrümmten Flugbahnen bewegen, traten hier die gleichen Berechnungsfehler auf. Die allgemeine Lehrmeinung dazu lautet, dass man hier die klassische Geometrie verlassen und sich der sogenannten Manhattan-Metrik zuwenden muss, um die Quantengleichungen zu lösen. Das ist interessant, denn in der Manhattan-Metrik gilt Pi = 4.
Manche erheben Einwände gegen diese meine Aussage. Sie sagen, Pi sei 3,14… und könnte daher nicht 4 sein. Ihrer Meinung nach sollte ich zumindest einen anderen griechischen Buchstaben verwenden. Pi ist jedoch nicht als 3,14 … definiert, sondern als Verhältnis des Umfangs eines Kreises zu seinem Durchmesser.
Ich habe bewiesen, dass dieses Verhältnis in Bewegung 4 ist. Daher ist die Aussage Pi = 4 korrekt.
Andere meinen, dies sei Haarspalterei, in den meisten Fällen wäre Pi immer noch 3,14 … Das ist jedoch schlicht falsch. In der Physik – und daher auch in der Realität – beinhalten fast alle Anwendungsfälle für Pi Bewegung. Wird Pi in physikalischen Gleichungen eingesetzt, ist in 99 Prozent der Fälle irgendeine Form von Umlaufgeschwindigkeit im Spiel. Aus diesem Grund lautete der Titel des Originalartikels provokant: „Die Vernichtung von Pi“. In wenigen Jahren wird die Zahl 3,14 … nur noch ein gedankliches Relikt sein.
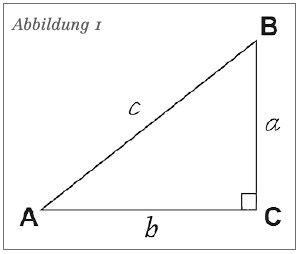
Ich werde versuchen, das so einfach wie möglich zu erklären. Um sich auf einer Kurvenbahn zu bewegen, müssen zwei Bewegungen ausgeführt werden. Sie müssen sich vorwärts und seitwärts zugleich bewegen, richtig? Gehen wir daher also von einem rechtwinkeligen Dreieck aus (Abbildung 1).
Sagen wir, die Punkte A und B befinden sich auf einer Kreisbahn und Sie möchten von A nach B gelangen. Die einfachste Variante scheint der direkteste Weg entlang der Geraden c zu sein. Sie bewegen sich also geradeaus auf der Hypotenuse. Genau das nahmen die alten Griechen tatsächlich an. Diese ursprüngliche Annahme führte seither zur Verzerrung des Problems und ist auch heute noch gültig.
Der Großteil der Mathematiker und Physiker geht immer noch davon aus, dass ein Kreis aus einer unendlich großen Anzahl kleinerc-Geraden besteht. Die einzelnenc-Geraden werden unendlich verkleinert und dann addiert, um den Umfang eines Kreises zu erhalten. Ich konnte jedoch beweisen, dass es sich dabei um eine bewusste Täuschung handelt. Sie können sich gar nicht entlang der Geraden c bewegen, weil diese die gleichzeitige Bewegung vorwärts und seitwärts, über die wir vorhin gesprochen haben, nicht korrekt abbildet.
Offensichtlich repräsentiert Geradeadie Vorwärtsbewegung und Geradebdie Seitwärtsbewegung. Egal wie klein das Dreieck ist, Sie müssen sich immer entlang der Geraden a und b bewegen.
Nun meinen Sie vielleicht: „Das kann gar nicht stimmen! Ich kann die Dreiecke doch auf den Boden zeichnen und mich immer entlang der Hypotenuse bewegen. Es gibt keinen Grund, das nicht zu tun.“ Stimmt. Aber wenn Sie sich immer entlang der Hypotenuse bewegen, bewegen Sie sich nicht wirklich entlang einer Kurve, oder?
Sie bewegen sich auf einer geraden Linie. Selbst wenn Sie sehr vielec-Geraden miteinander verbinden, sodass ein Kreis entsteht, ist das kein echter Kreis. Es ist ein Vieleck. Sogar wenn Ihr Kreis aus tausenden von kleinenc-Geraden besteht, schneiden Sie die Eckejedes Minidreiecks ab. Wenn Sie aber die Ecken schneiden, bilden Sie mit Ihrem sogenannten „Kreis“ keine gleichzeitige Vorwärts-Seitwärts-Bewegung ab. Es ist also kein echter Kreis. Und es entsteht keine echte Kreisbewegung.
Sie werden nun einwenden: „Das mag ja stimmen, aber wenn ich die Hypotenusen klein genug mache, erhalte ich trotzdem das richtige Ergebnis für den Umfang des Kreises. Das weiß doch jedes Kind.“ In diesem Fall ist das, was jedes Kind „weiß“, allerdings falsch. Wenn Sie all die Ecken der unzähligen kleinen Dreiecke abkürzen, ist das für den Kreisumfang erhaltene Ergebnis viel zu gering. Genauer gesagt: um 21 Prozent zu gering – eine ganze Menge. Es handelt sich also nicht nur um eine minimale Abweichung; es ist ein gewaltiger Fehler.
Das mag Ihnen immer noch unverständlich scheinen. In meinen anderen Arbeiten habe ich diesen Zusammenhang viel ausführlicher und mit detaillierteren Berechnungen erklärt. Falls Sie mir allerdings hier schon nicht folgen konnten, können Sie es in diesen Arbeiten wahrscheinlich auch nicht. Unabhängig davon ist die einfachste Antwort auf die Frage, warum eine Kugel in einer kreisförmigen Röhre so lange für eine Umrundung braucht: weil sie die Ecken nicht abkürzt. Die Kugel bewegt sich nicht entlang derc-Geraden. Sie folgt den Geraden a und b.
[Die Animation im YouTube-Video unter http://tinyurl.com/h8amdf2 zeigt, wie aus rechtwinkeligen Geraden eine Kreisbewegung entsteht.]
Falls unter Ihren Freunden Mathematiker sind, werden Ihnen diese erzählen, Sie müssten etwas von Infinitesimalrechnung verstehen, um das zu begreifen. Das ist allerdings nur ein Trick. Ich habe Ihnen oben ganz ohne Infinitesimalrechnung erklärt, warum das stimmt. Wie auch immer, ich sage Ihnen hier nur, was Ihre Mathematikerfreunde erzählen werden. Sie werden erklären, man erhielte durch die Integration der Geraden a und b die Gerade c.
Integralrechnung ist Teil der Infinitesimalrechnung. Ihre Verwendung an dieser Stelle ist zwar richtig, doch wenn Sie korrekt integrieren, erhalten Sie als Ergebnis nicht die Geradec.
Damit wird derzeit zwar die richtige Berechnungsmethode für dieses Problem herangezogen, jedoch in der falschen Art und Weise. Und ich kann Ihnen das möglicherweise erklären, ohne Ihnen zuerst Integralrechnung beizubringen.
Die Zeitvariable
Die Abbildung des Dreiecks weiter vorn stellt eine Vereinfachung des Problems dar, weil Zeit dabei nicht berücksichtigt wird. Es ist eine rein geometrische Betrachtung. Obwohl die Darstellung also soweit richtig ist, verdeutlicht sie nicht das gesamte Problem. Das Dreieck hilft Ihnen, zu verstehen, warum die Kugel nicht der Geraden c folgen kann. Es zeigt Ihnen aber nicht, wie die Kugel die beiden Bewegungen zu einer Kurve kombiniert.
Eben haben Sie festgestellt, dass die Kugel die Geraden a und b nichtverbindet. Mit anderen Worten, sie werden nicht auf irgendeine mathematisch-magische Art integriert. Egal wie klein die Strecken werden und egal wie viele kleine Dreiecke Sie auf der Kreislinie zeichnen, die Geraden a und b sind stets klar erkennbar und stehen im rechten Winkel zueinander. Sie verbinden sich nie zu einerc-Geraden.


 In einer Reihe wissenschaftlicher Arbeiten habe ich bereits erklärt, warum für Bewegung gilt Pi (π) = 4. In diesem Artikel hier möchte ich dies nun für alle, die entweder nur wenig von Mathematik verstehen oder sich nicht genauer damit auseinandersetzen wollen, vereinfacht darstellen. Viele Menschen werden an dieser Stelle lachen und etwas sagen wie: „Ich wusste gar nicht, dass es hier überhaupt etwas zu lösen gab!“ Doch es gibt Probleme, und Insider wissen davon.
In einer Reihe wissenschaftlicher Arbeiten habe ich bereits erklärt, warum für Bewegung gilt Pi (π) = 4. In diesem Artikel hier möchte ich dies nun für alle, die entweder nur wenig von Mathematik verstehen oder sich nicht genauer damit auseinandersetzen wollen, vereinfacht darstellen. Viele Menschen werden an dieser Stelle lachen und etwas sagen wie: „Ich wusste gar nicht, dass es hier überhaupt etwas zu lösen gab!“ Doch es gibt Probleme, und Insider wissen davon.
Kommentar schreiben