NEXUS Magazin: https://www.nexus-magazin.de/artikel/lesen/ein-einfaches-experiment-beweist-4
In einer Reihe wissenschaftlicher Arbeiten habe ich bereits erklärt, warum für Bewegung gilt Pi (π) = 4. In diesem Artikel hier möchte ich dies nun für alle, die entweder nur wenig von Mathematik verstehen oder sich nicht genauer damit auseinandersetzen wollen, vereinfacht darstellen. Viele Menschen werden an dieser Stelle lachen und etwas sagen wie: „Ich wusste gar nicht, dass es hier überhaupt etwas zu lösen gab!“ Doch es gibt Probleme, und Insider wissen davon.
Sowohl in der Raketenforschung als auch in der Quantenmechanik traten in Zusammenhang mit Pi große Probleme auf. Vor mir hatte jedoch noch niemand Pi selbst infrage gestellt.
In der Raumfahrt stellten die Techniker von Beginn an ein Versagen ihrer theoretischen Gleichungen in der Praxis fest. Ende der 1950er Jahre gestanden Wissenschaftler des amerikanischen Raumfahrtprogramms unter der Leitung von Dr. Wernher von Braun massive Fehler in ihren Berechnungen ein. Die Raketen waren einfach nicht dort, wo sie sein sollten – allerdings nur,wenn gekrümmte Flugbahnen im Spiel waren. Die ersten Raketen in der Erdumlaufbahn wiesen massive Verspätungen auf, was auf Berechnungsfehler von über 20 Prozent hindeutete. Die Russen standen vor demselben Problem.
In den Pressemitteilungen verwiesen sie – und tun das immer noch – auf ein mögliches Treibstoffproblem. Hinter den Kulissen aber untersuchten sie andere Möglichkeiten. Heute wird das Versagen der Gleichungen Dunkler Materie zugeschrieben. In den 1960er Jahren fragten sich die Wissenschaftler, ob das Problem mit den Raketen von unbekannten Äthern oder anderen Naturgewalten stammen könnte. Wie sich herausstellte, entsprechen die Fehler in den Gleichungen genau der Differenz zwischen Pi und 4.
Ein ganz ähnliches Problem zeigte sich in der Quantenmechanik. Da sich Quanten oft auf Umlaufbahnen oder gekrümmten Flugbahnen bewegen, traten hier die gleichen Berechnungsfehler auf. Die allgemeine Lehrmeinung dazu lautet, dass man hier die klassische Geometrie verlassen und sich der sogenannten Manhattan-Metrik zuwenden muss, um die Quantengleichungen zu lösen. Das ist interessant, denn in der Manhattan-Metrik gilt Pi = 4.
Manche erheben Einwände gegen diese meine Aussage. Sie sagen, Pi sei 3,14… und könnte daher nicht 4 sein. Ihrer Meinung nach sollte ich zumindest einen anderen griechischen Buchstaben verwenden. Pi ist jedoch nicht als 3,14 … definiert, sondern als Verhältnis des Umfangs eines Kreises zu seinem Durchmesser.
Ich habe bewiesen, dass dieses Verhältnis in Bewegung 4 ist. Daher ist die Aussage Pi = 4 korrekt.
Andere meinen, dies sei Haarspalterei, in den meisten Fällen wäre Pi immer noch 3,14 … Das ist jedoch schlicht falsch. In der Physik – und daher auch in der Realität – beinhalten fast alle Anwendungsfälle für Pi Bewegung. Wird Pi in physikalischen Gleichungen eingesetzt, ist in 99 Prozent der Fälle irgendeine Form von Umlaufgeschwindigkeit im Spiel. Aus diesem Grund lautete der Titel des Originalartikels provokant: „Die Vernichtung von Pi“. In wenigen Jahren wird die Zahl 3,14 … nur noch ein gedankliches Relikt sein.
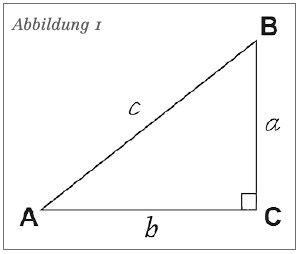
Ich werde versuchen, das so einfach wie möglich zu erklären. Um sich auf einer Kurvenbahn zu bewegen, müssen zwei Bewegungen ausgeführt werden. Sie müssen sich vorwärts und seitwärts zugleich bewegen, richtig? Gehen wir daher also von einem rechtwinkeligen Dreieck aus (Abbildung 1).
Sagen wir, die Punkte A und B befinden sich auf einer Kreisbahn und Sie möchten von A nach B gelangen. Die einfachste Variante scheint der direkteste Weg entlang der Geraden c zu sein. Sie bewegen sich also geradeaus auf der Hypotenuse. Genau das nahmen die alten Griechen tatsächlich an. Diese ursprüngliche Annahme führte seither zur Verzerrung des Problems und ist auch heute noch gültig.
Der Großteil der Mathematiker und Physiker geht immer noch davon aus, dass ein Kreis aus einer unendlich großen Anzahl kleinerc-Geraden besteht. Die einzelnenc-Geraden werden unendlich verkleinert und dann addiert, um den Umfang eines Kreises zu erhalten. Ich konnte jedoch beweisen, dass es sich dabei um eine bewusste Täuschung handelt. Sie können sich gar nicht entlang der Geraden c bewegen, weil diese die gleichzeitige Bewegung vorwärts und seitwärts, über die wir vorhin gesprochen haben, nicht korrekt abbildet.
Offensichtlich repräsentiert Geradeadie Vorwärtsbewegung und Geradebdie Seitwärtsbewegung. Egal wie klein das Dreieck ist, Sie müssen sich immer entlang der Geraden a und b bewegen.
Nun meinen Sie vielleicht: „Das kann gar nicht stimmen! Ich kann die Dreiecke doch auf den Boden zeichnen und mich immer entlang der Hypotenuse bewegen. Es gibt keinen Grund, das nicht zu tun.“ Stimmt. Aber wenn Sie sich immer entlang der Hypotenuse bewegen, bewegen Sie sich nicht wirklich entlang einer Kurve, oder?
Sie bewegen sich auf einer geraden Linie. Selbst wenn Sie sehr vielec-Geraden miteinander verbinden, sodass ein Kreis entsteht, ist das kein echter Kreis. Es ist ein Vieleck. Sogar wenn Ihr Kreis aus tausenden von kleinenc-Geraden besteht, schneiden Sie die Eckejedes Minidreiecks ab. Wenn Sie aber die Ecken schneiden, bilden Sie mit Ihrem sogenannten „Kreis“ keine gleichzeitige Vorwärts-Seitwärts-Bewegung ab. Es ist also kein echter Kreis. Und es entsteht keine echte Kreisbewegung.
Sie werden nun einwenden: „Das mag ja stimmen, aber wenn ich die Hypotenusen klein genug mache, erhalte ich trotzdem das richtige Ergebnis für den Umfang des Kreises. Das weiß doch jedes Kind.“ In diesem Fall ist das, was jedes Kind „weiß“, allerdings falsch. Wenn Sie all die Ecken der unzähligen kleinen Dreiecke abkürzen, ist das für den Kreisumfang erhaltene Ergebnis viel zu gering. Genauer gesagt: um 21 Prozent zu gering – eine ganze Menge. Es handelt sich also nicht nur um eine minimale Abweichung; es ist ein gewaltiger Fehler.
Das mag Ihnen immer noch unverständlich scheinen. In meinen anderen Arbeiten habe ich diesen Zusammenhang viel ausführlicher und mit detaillierteren Berechnungen erklärt. Falls Sie mir allerdings hier schon nicht folgen konnten, können Sie es in diesen Arbeiten wahrscheinlich auch nicht. Unabhängig davon ist die einfachste Antwort auf die Frage, warum eine Kugel in einer kreisförmigen Röhre so lange für eine Umrundung braucht: weil sie die Ecken nicht abkürzt. Die Kugel bewegt sich nicht entlang derc-Geraden. Sie folgt den Geraden a und b.
[Die Animation im YouTube-Video unter http://tinyurl.com/h8amdf2 zeigt, wie aus rechtwinkeligen Geraden eine Kreisbewegung entsteht.]
Falls unter Ihren Freunden Mathematiker sind, werden Ihnen diese erzählen, Sie müssten etwas von Infinitesimalrechnung verstehen, um das zu begreifen. Das ist allerdings nur ein Trick. Ich habe Ihnen oben ganz ohne Infinitesimalrechnung erklärt, warum das stimmt. Wie auch immer, ich sage Ihnen hier nur, was Ihre Mathematikerfreunde erzählen werden. Sie werden erklären, man erhielte durch die Integration der Geraden a und b die Gerade c.
Integralrechnung ist Teil der Infinitesimalrechnung. Ihre Verwendung an dieser Stelle ist zwar richtig, doch wenn Sie korrekt integrieren, erhalten Sie als Ergebnis nicht die Geradec.
Damit wird derzeit zwar die richtige Berechnungsmethode für dieses Problem herangezogen, jedoch in der falschen Art und Weise. Und ich kann Ihnen das möglicherweise erklären, ohne Ihnen zuerst Integralrechnung beizubringen.
Die Abbildung des Dreiecks weiter vorn stellt eine Vereinfachung des Problems dar, weil Zeit dabei nicht berücksichtigt wird. Es ist eine rein geometrische Betrachtung. Obwohl die Darstellung also soweit richtig ist, verdeutlicht sie nicht das gesamte Problem. Das Dreieck hilft Ihnen, zu verstehen, warum die Kugel nicht der Geraden c folgen kann. Es zeigt Ihnen aber nicht, wie die Kugel die beiden Bewegungen zu einer Kurve kombiniert.
Eben haben Sie festgestellt, dass die Kugel die Geraden a und b nichtverbindet. Mit anderen Worten, sie werden nicht auf irgendeine mathematisch-magische Art integriert. Egal wie klein die Strecken werden und egal wie viele kleine Dreiecke Sie auf der Kreislinie zeichnen, die Geraden a und b sind stets klar erkennbar und stehen im rechten Winkel zueinander. Sie verbinden sich nie zu einerc-Geraden.
Sie fragen sich sicher, wofür wir die Integralrechnung brauchen? Weil wir, um dieses Problem zu lösen, die Geradenaundbmit der Zeittintegrieren müssen. Anders gesagt: Wir integrieren nichtaundb. Wir integrierenamittund dannbmit demselben Wert vont. Falls Ihnen das Wort „integrieren“ nicht zusagt – weil es sich dabei um einen Begriff der Infinitesimalrechnung handelt – lassen Sie es mich so ausdrücken: Wir müssen nachvollziehen, wie sich erstaund dannbim Zeitraumtändern. So berücksichtigen wir auch den Zeitfaktor dieses Problems.
Versuchen Mathematiker oder Physiker gegenwärtig, das Problem mittels Integralrechnung zu lösen, lassen sie die Zeit mehr oder weniger außen vor und messenaim Verhältnis zub. Sie integrieren Bewegungamit Bewegungb, um Bewegungczu erhalten. Bewegungcentspricht derc-Geraden. Doch obwohl die genutzte Berechnungsmethode an sich korrekt ist, wird sie falsch umgesetzt. Da die gesamte Physik im Prinzip angewandte Mathematik ist, muss die Mathematik jedoch richtig angewandt werden. Wird die richtige Berechnungsmethode falsch eingesetzt, liefert sie trotz allem ein falsches Ergebnis.
In meinen anderen Arbeiten habe ich daher Rollkurven-Berechnungen als Lösung vorgeschlagen. Eine Rollkurve ist ein zyklischer oder rollender Kreis. Rollkurven-Berechnungen sind an dieser Stelle hilfreich, weil sie explizit die Zeit miteinbeziehen. Die Berechnungsmethode integriert die drei Variablen a, b und t. Darüber hinaus werden die Variablen in der Rollkurven-Berechnung auch richtig eingesetzt. Wir müssen also nur noch die Rollkurven-Berechnung nehmen und sie auf der Strecke entlang der Kreisbahn anwenden. Das löst unser Problem perfekt und liefert uns die richtige Antwort: Der Umfang eines Kreises ist 8r.
Warum funktioniert die Rollkurven-Berechnung hier? Die Bewegung entlang einer Kreislinie gleicht der Bewegung entlang der Außenseite eines um seinen Mittelpunkt rotierenden Kreises. Anders ausgedrückt: Stellen Sie sich ein großes, sich drehendes Hamsterrad vor, das fixiert ist und sich daher nicht vorwärtsbewegt. Es dreht sich einfach auf der Stelle. Sie befinden sich an einer beliebigen Stelle an der Außenseite des Rads. Während sich das Rad dreht, drehen Sie sich ebenfalls – nun vollführen Sie eine Kreisbewegung. Genau das bildet die moderne Rollkurven-Berechnung ab.
Unabhängig davon versteht ein Großteil der Menschen nicht, wie ich auf die Idee kam, so etwas infrage zu stellen. Ich bin kein berühmter Quantenphysiker oder Wissenschaftler der NASA. Und ich gebe zu, ich hatte keine Ahnung von den Problemen in der Quantenphysik und Raketenforschung, als ich dies berechnete. Sie waren nur eine nachträgliche Bestätigung der Fakten. Ich wusste nichts über von Brauns Probleme mit den Gleichungen, bis ich meine Arbeiten über Pi geschrieben hatte. Die Verbindung zur Rollkurven-Berechnung – wo Pi ebenfalls gleich 4 ist – entdeckte ich erst einige Jahre später. Wie also konnte ich ein Problem lösen, von dem ich gar nicht wusste, dass es existierte?
Nun, ich kam über Umwege dorthin, als ich damit zusammenhängende Probleme lösen sollte. Und ein Zusammenhang zwischen den Problemen war vorhanden. Doch niemand wusste davon, bis ich ihn aufzeigte. Ich arbeitete damals an Newtons Gleichungen zur Umlaufbahnbestimmung, die meiner Meinung nach einige Unklarheiten aufwiesen. Anders ausgedrückt: Sie ergaben für mich keinen Sinn. Newtons Beweise waren in meinen Augen ziemlich lückenhaft und die neueren Versionen der Beweisführung durch Größen wie Dr. Richard Feynman erschienen mir um nichts besser. Tatsächlich konnte ich sogar nachweisen, dass diese schlechter waren.
Da es sich bei einer Umlaufbahn nur um eine Bewegung entlang eines Kreises handelt, lässt sich der Zusammenhang einfach erkennen. Ich begann also noch einmal ganz von vorne und löste Newtons Gleichungen ein zweites Mal, diesmal mit ein paar Korrekturen. Die Korrekturen lösten viele Probleme, aber nicht alle. Doch ich sollte erst ein paar Jahre später auf den Gedanken kommen, Pi selbst genauer zu betrachten.
Meine Korrekturen an den Gleichungen zur Bahnbestimmung deuteten darauf hin, dass der Wert von Pi einfach nicht korrekt war. Wie sich herausstellte, basierten die alten Gleichungen zur Bahnbestimmung – auch jene von Newton – auf der euklidischen Geometrie, die Zeit außen vor ließ. Die in der Schule gelehrte Geometrie berücksichtigt keine Geschwindigkeiten. Sie umfasst nur Distanzen. Wird Pi mithilfe der Geometrie – ohne Zeit und Geschwindigkeiten – berechnet, lautet das Ergebnis tatsächlich 3,14 … In der Physik ist diese Art der Berechnung jedoch unbrauchbar. In der Physik gibt es fast immer eine Bewegung, die nachvollzogen werden soll. Zeit spielt also immer eine Rolle. Jede Streckenlänge muss durch eine Geschwindigkeit ersetzt werden. Und sobald Sie das tun, können Sie die euklidische Geometrie nicht mehr nutzen. Sie enthält einfach nicht genug Variablen – man hat immer eine Variable zu wenig.
Das bedeutet aber auch, die alten Berechnungen zur Umlaufbahnbestimmung hatten immer eine Variable zu wenig. Sie waren unvollständig, in ihnen fehlte die Zeit. Weil in den Berechnungen aber die Zeit fehlte, konnten sie die Realität nicht abbilden. Sie funktionierten nur für ein theoretisches Konstrukt, wo alles in einem einzigen imaginären Moment stattfand. Am Ende wurden dadurch alle Berechnungen unlösbar.
In der Quantenmechanik gibt es die sogenannte Renormierung. Dieses Verfahren wird dort für nicht lösbare Gleichungen angewendet. Vereinfacht gesagt: Sollen Probleme aus der Realität mit Gleichungen ohne ausreichende Berücksichtigung der Zeitvariablen berechnet werden, liefern die Gleichungen nur null oder unendlich als Lösungen. In der Quantenmechanik ist das bei allen Gleichungen der Fall. Das gestehen die Forscher ein, wissen aber nicht, warum. Anders formuliert versuchen sie, kinematische Probleme mit Geometrie zu lösen. Das ähnelt dem Versuch, ein Ölgemälde mit dem Bleistift zu malen.
Entsprechend können auch keine physikalischen Probleme mit Geometrie gelöst werden, da auch dafür die Zeitvariable fehlt. Zwar wird versucht, die Zeit am Ende irgendwie wieder in die Berechnungen einzufügen, doch dies hat noch nie funktioniert.
Quelle: überarbeitete Version des vollständigen Artikels auf der Webseite http://milesmathis.com/pi7.pdf
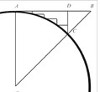
Gegeben ist ein Kreissegment entsprechend der Abbildung mit AO = AB. Damit ist der Winkel bei B gleich 45 Grad und es gilt DB = DC.
Daraus folgt durch Substitution AD + DC = AB. Die Strecke AD + DC kann auch als jede beliebige Zahl an Teilstrecken dargestellt werden, wie in der Abbildung eingezeichnet. Hier ist der Weg in vier Teilstrecken gegliedert, die uns in vier Stufen von A nach C bringen.
Der neue Weg, vorgegeben von den Teilstrecken, hat dieselbe Länge wie AD + DC. Das ist auch bei flüchtiger Betrachtung erkennbar. Sie liegt näher am Kreisbogen AC, doch die Länge entspricht immer noch der Originalstrecke AD + DC.
Unterteilen wir den Weg in acht Teilstücke statt in vier, bleiben wir noch näher am Kreisbogen, behalten aber wieder die ursprüngliche Länge von AD + DC bei.
Wenn wir uns mit diesem Verfahren Richtung Grenzwert bewegen, nähern wir unseren Weg dem Kreisbogen AC an. Das muss also bedeuten, die Länge des Kreisbogens AC ist gleich der Streckenlänge AD + DC. Aufgrund der Substitutionsregeln bedeutet das: AC = AB.
Da ein Kreis aus acht solchen Bögen besteht, ergibt sich daraus der Umfang des Kreises mit 8AB.
Weil AB = AO und AO dem Radius entspricht, lautet die Formel also U = 8r.
Pi kommt in der Kreisgleichung hier nicht vor und wurde somit ausgelöscht.
Einige mögen nun einwerfen, meine Berechnungen seien falsch. Ich behaupte jedoch, nicht ich, sondern alle bisherigen Mathematiker haben falsch gerechnet.
Die übliche Reaktion auf meine Darstellung oben lautet, dass beim Grenzwert nach seiner derzeitigen Definition die Gesamtlänge der Stufen den Kreisbogen nie erreicht. Denn selbst bei einer unendlich großen Zahl an Schritten bleibt immer noch ein realer Abstand zwischen der Kreislinie und den einzelnen Stufen. Diesen Abstand können wir auch beim Grenzwert noch aufsummieren, dadurch ist die Summe der Stufen-Strecken stets höher als die Länge der Kurve. Aber nicht die Summe der Stufen-Strecken wird der Kurve angenähert; die Kurve wird den Kreissehnen angenähert. In anderen Worten: Es sind die Hypotenusen der kleinen Dreiecke, die gegen die Kurve konvergieren, nicht die Summe der anderen Seiten des Dreiecks.
Obwohl mir bewusst ist, dass es sich hier um die gängige Meinung handelt, kann ich ihr nicht zustimmen. In meiner Arbeit über die newtonschen Hilfssätze (zu finden auf meiner Webseitehttp://tinyurl.com/h9kxaal) habe ich nachgewiesen, dass die Tangente seines Dreiecks am Grenzwert länger sein muss als die Kreissehne und damit der Kreisbogen. Wenn wir das auf dieses Problem umlegen, bedeutet das, der Kreisbogen kann sich der Kreissehne des Grenzwerts gar nicht annähern. Die Tangente ist laut Newtons eigener Definition in der Principia ein Teil des Kreisbogens. Wenn also die Tangente am Grenzwert länger ist als die Kreissehne, muss das auch für den Kreisbogen gelten.
Das heißt, die Kurve nähert sich in keinem Fall den Hypotenusen der Stufen an, egal wie viele es sind. Die Hypotenusen sind die Kreissehnen und sowohl Kreisbogen als auch Tangente konvergieren nicht gegen sie.
Sie wollen nun sicher wissen, wo in der Principia Newton schreibt, der Kreisbogen bestünde aus Tangenten. An derselben Stelle, an der er erklärt, die Kreisbewegung bestünde aus den Vektoren der zentripetalen Beschleunigung und der Eigenbewegung eines Körpers. Newton definiert nur diese beiden Bewegungen, und er ordnet die Eigenbewegung des Körpers explizit der Tangente zu.
Damit können aber die historischen und gegenwärtigen Interpretationen nicht korrekt sein. Die Hypotenusen konvergieren nicht gegen Kurve oder Kreisbogen. Wie in der Abbildung gezeigt, nähert sich die Tangente dem Kreisbogen an, allerdings nur, wenn die Tangentenlänge gleich dem Radius ist. Das wiederum ist nur der Fall, wenn das Segment einem Achtel des Kreises entspricht. Die Annäherung erfolgt dann genau wie in meinen Arbeiten beschrieben, weil der Kreisbogen auch am Grenzwert niemals eine stetige Kurve ist.
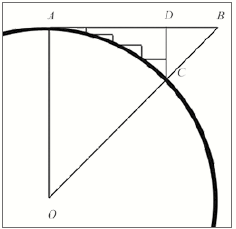
Ein Kreisbogen ist definiert als eine aus geraden oder linearen Vektoren bestehende Kurve und kann daher nicht stetig sein, sofern wir unter „stetig“ verstehen, dass zurückgelegter Weg oder vergangene Zeit gegen null gehen. Logischerweise können Weg und Zeit nicht gegen null gehen, da es bei null weder Weg noch Zeit gibt. Alle Zahlen in der Mathematik und Physik beinhalten ein Differenzial; und weil das so ist, kann eine Kurve auch nicht als ununterbrochen in diesem Sinne gelten. Eine Kurve muss auch am Grenzwert als Ergebnis linearer Vektoren betrachtet werden.
Da dies so sein muss, muss auch stimmen, dass sich der von mir in der Abbildung gezeichnete Weg dem Kreisbogen annähert, und zwar aus genau den von mir genannten Gründen. Der Weg nähert sich dem Kreisbogen in dem Sinne an, als er tatsächlich näher an den Bogen herankommt. Das zumindest kann niemand abstreiten. Weil aber der Kreisbogen nicht einmal am Grenzwert stetig ist, konvergiert der Weg tatsächlich gegen den Kreisbogen, je mehr Stufen wir einzeichnen.
Weil sich aber die Streckenlänge nie ändert, egal wie viele Stufen wir zeichnen, muss die Tangente gegen den Kreisbogen konvergieren. Oder, betrachtet man einen Achtel eines Kreises, muss die Tangente schlicht der Kreisbogen sein.
Quelle: redaktionelle Aufbereitung der Webseite http://milesmathis.com/pi3.html
Viele Leser, besonders jene, die gerade erst auf meine Arbeiten gestoßen sind, werden bei diesem Artikel früher oder später in eine gedankliche Sackgasse geraten. Wer tatsächlich mit diesem Artikel beginnt, kommt höchstwahrscheinlich zu dem Schluss, ich würde die Integrale falsch berechnen. Diesen Menschen möchte ich entgegnen, dass nicht ich es bin, der die Integrale falsch berechnet. Newton und Leibniz und Cauchy und alle Mathematiker danach haben die Integrale falsch berechnet. Indem ich drei bedeutende Arbeiten über die Grundlagen der Infinitesimalrechnung schrieb, habe ich mir das Recht erarbeitet, diesen Artikel hier zu schreiben.
Der erste Artikel1 zeigt auf, dass die Ableitungsfunktion von Beginn an falsch definiert wurde. Die Ableitung ist ein konstantes Differenzial in einem Teilintervall und kein bei der Annäherung an null unendlich klein werdendes Differenzial. Die Annäherung an null in der Differenzialrechnung ist unnötig und das Intervall der Ableitung ist eine real existierende Differenz. In jedem spezifischen Problem findet sich auch Zeit, die im Intervall der Ableitung vergeht. In der Differenzialrechnung ist also ebenfalls nichts momentan. Das revolutioniert die Quantenelektrodynamik, weil dadurch das Idealteilchen ausgeschlossen und die Notwendigkeit der Renormierung umgangen wird.
Der zweite Artikel2 beweist, dass die ersten acht Hilfssätze oder Annahmen von Newton in der Principia Mathematica alle falsch sind. Newton betrachtet bei der Annäherung an den Grenzwert den falschen Winkel seines Dreiecks. Dadurch zieht er falsche Schlüsse bezüglich der Winkel sowie über die Tangenten- und Bogenlänge des Grenzwerts.
Der dritte Artikel3 schließlich setzt sich gründlich mit den historischen Beweisführungen für die Kreisbeschleunigungsformel a = v2/r auseinander. Die Arbeit umfasst auch die Beweisführung von Newton und Feynman und zeigt, dass sie alle fundamentale Fehler enthielten. Die derzeit gültige Gleichung dafür wird ebenso wie die Formel für die Kreisgeschwindigkeit v = 2πr/t falsifiziert.
Wem also der Artikel hier zu ungenau oder zu wenig mathematisch ist, sollte diese Arbeiten lesen, bevor das alles als „eine Nummer zu groß“ abgetan wird. Ich kann unmöglich in jeder Arbeit alle meine Beweise herleiten oder alle meine Argumente aufzählen. Ich fürchte also, wer sich wirklich überzeugen lassen will, wird noch etwas weiterlesen müssen.
Dieser Artikel baut allerdings auf die in den anderen Arbeiten enthaltenen Änderungen historischer Formeln auf, das muss ich an dieser Stelle zugeben.
Quelle: redaktionelle Aufbereitung der Webseite http://milesmathis.com/pi2.html